顾客满意度的研究最早始于20世纪80年代初的美国和日本,顾客满意度是顾客对企业的产品或服务所预期的价值与所感知的价值之间的对比,也就是企业所提供的产品或服务与顾客期望或要求相吻合的程度。顾客满意度是顾客感觉状态的一种水平,是期望获得的价值与感知到的价值之间的差距。这里“顾客满意度、价值感知、顾客期望”等变量是无法直接进行测量和分析的,它们都是潜变量,与之对应能够直接进行测量和分析的就称为是显变量。而潜变量模型,如因子分析和结构方程模型,就是探讨观测到的变量与潜变量之间关系的模型,在一定程度上符合社会学、心理学等的理论,并是随着统计软件发展被这些应用学科所广泛采用。
一、研究背景及问题提出
在市场调查和市场研究中,多采用结构方程模型来探索顾客满意度的构成要素及其对顾客忠诚度的影响,这里所说的结构方程即统计学上的基于正态分布的线性潜变量模型。然而在顾客满意度研究的实践中,我们发现有时线性的模型假定并不符合某些实际数据,对这样的数据,普通的结构方程模型就失效了。
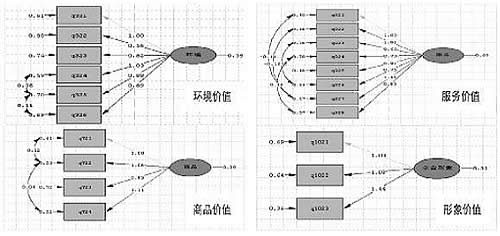
S公司是一家大型的百货零售企业,年销售额超过20亿美元。近年来,S公司越来越受到新兴零售企业竞争的威胁,原来忠诚的老客户开始流失,顾客的抱怨时有发生。商场运营管理部为了进一步改善顾客服务质量,增强企业竞争力,引进了顾客满意度测评,作为改善日常经营管理工作的重要工具。2002年10月,S公司与某管理顾问公司联手对顾客满意度进行了测评。在进行了一系列的焦点小组访谈和深度访谈后,参照已有的顾客满意度研究资料,确定了影响顾客满意度的关键维度,并确定了每个维度包括的测量指标。接下来,S公司与某管理顾问公司共同设计了定量调研问卷和抽样调查方案,采用拦截访问的方式总共采集有效样本900个。从900个有效样本中随机抽取800个作为本文的分析数据。通过因子分析得到5个潜变量Satis(满意程度),Environment(环境价值),Goods(商品价值),Service(服务价值),Vision(形象价值),其中商品价值、形象价值、环境价值和服务价值的测量模型如下所示:
在获得上述5个潜变量之后,进一步的数据分析结果表明:所有顾客的“环境价值”与“满意程度”之间没有预期的单调关系,对那些“环境价值”感知偏低的顾客,他们的“满意程度”反而高,而对那些“环境价值”感知不太低的顾客,他们的“满意程度”倒随“环境价值”感知的提高而增加。这一现象说明,“满意程度”与“环境价值”之间可能存在非线性的关系。另外,数据分析的结果也表明,年龄这个变量是人口统计变量中一个不可忽视的影响顾客满意度的显变量,那么年龄是怎样与其他4个潜变量一起对顾客的满意程度产生影响的呢?
上述问题很难在普通结构方程模型框架下得到解决。针对这种状况,下文提出半参数潜变量回归模型,并将此模型应用到S公司2002年度的顾客满意度研究数据中,模型的惩罚样条估计和限制似然比检验均编写成R程序,该程序的运行结果表明,本文所提的半参数模型与线性潜变量模型相比,对数据的拟合更好一些。
二、半参数潜变量回归模型及其在顾客满意度研究中的应用
考虑半参数潜变量模型 ,其中
独立同 且与Z和X独立,X是协变量向量且其中部分分量是显变量,Z是另外协变量也是潜变量,f(Z)是光滑非线性函数。对非参数部分f(Z)的估计方法有很多,本节采用的是P样条光滑并以AIC准则来选择光滑参数。P样条是一种固定结点光滑方法,基底函数的维数固定并事先确定,所以估计是一个同时完成变量选择和光滑参数选择的过程,另外在P样条方法下,半参数潜变量模型可表示成线性混合效应模型,其中光滑参数是随机效应的方差,因而模型的失拟诊断就是随机效应是否0方差的检验。
考虑样条函数,
其中 为回归系数向量,
是固定节点, 是相应于z的
的样本分位点。令 ,X的行向量为,
W的是行向量为 , S的行向量为
, ,
。将 和 看作固定参数,b为随机参数且均值为零,协方差矩阵为 。若 是正态随机变量,b和 独立, , 是光滑参数,则上述半参数潜变量模型变为: 。
于是在线性混合效应模型的框架下,可得半参数潜变量模型的最优线性无偏估计(预测)。
针对本文案例,对上节提到的S公司的顾客满意度研究数据,将满意程度(Satis)这一潜变量作为因变量,将年龄(age)这一显变量和其余4个潜变量:环境价值(Environment)、商品价值(Goods)、服务价值(Service)和形象价值(Vision)作为自变量,拟合半参数潜变量模型,其中满意程度(Satis)与环境价值(Environment)之间的存在非线性关系,满意程度(Satis)与商品价值(Goods)、服务价值(Service)、形象价值(Vision)和年龄(age)间存在线性关系:satis=f(Environment)+?酌1*Goods+?酌2*Service+?酌3*Vision+?酌4*age+?着。
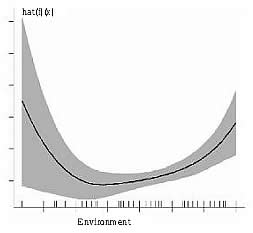
模型的估计:运行编写好的R程序,得到上述模型中线性回归系数的极大似然估计,分别为0.2082,0.1398,0.3185,0.13569,经检验这4个估计均显著,未知函数f(Environment)的P样条光滑估计如下图所示。
模型的失拟诊断:即上面得到的半参数潜变量模型线性潜变量模型相比,哪个模型能够更好地拟合数据。首先,我们得到针对800个随机抽出数据的线性潜变量模型,然后,运行编写的R程序得到,限制似然比检验统计量的值为1.564,基于5000个模拟数据的P-值为0.0192,检验结果表明,半参数潜变量模型与线性潜变量模型相比,半参数潜变量模型能够更好地拟合S公司2002年的顾客满意度调查数据。