【研究背景】
嘉泰公司是一家中型飞机零件制造企业,雇有500多名生产工人担任不同水平的职位和技术工作。近年来,随着嘉泰公司的销售额稳定上升,公司的管理层开始关心企业中(尤其是生产第一线上)缺勤率很高的问题。嘉泰公司的人事经理估计,在2006年一年中,平均雇员缺勤次数超过两次,每次缺勤持续1天以上。
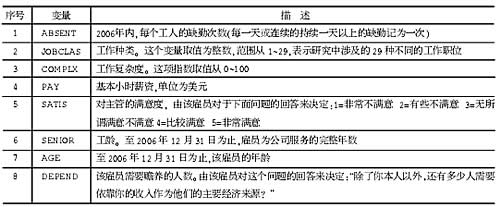
为了处理车间缺勤问题,嘉泰公司管理层聘请管理咨询公司对影响工人缺勤率的因素进行研究,目的是要确定影响嘉泰公司雇员缺勤率的主要因素。管理咨询公司的咨询顾问通过对嘉泰公司生产运作流程的观察后,对几名生产线上的主管和雇员进行了小组访谈与深度访谈,定义了一个名为ABSENT的变量,用来衡量缺勤程度,此外还有7个变量,具体情况如下。咨询顾问随机地从嘉泰公司中挑选了77名雇员,从他们中收集了8个变量的数据。
一、拟合模型
在对调查所得基础数据进行探索性分析的基础上,通过如下分析,得到最终的拟合模型:
第一,对自变量COMPLX和SENIOR进行对数函数变换;
第二,对变量SATIS重新进行分类,引入新的二元指示哑变量SATIS_M,分别代表“对主管有意见”和“对主管无意见”;
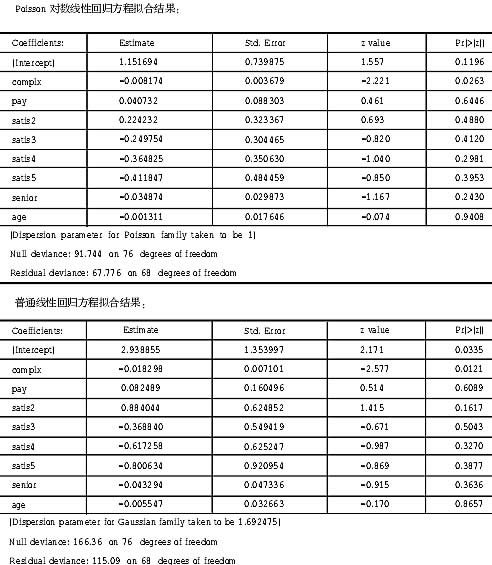
第三,由于ABSENT是一个计数因变量,不满足普通线性回归方程拟合中正态因变量的假定,因此从严格的意义上说,本案数据不能建立普通线性回归方程。同时,由于变量ABSENT的均值和方差分别约为2.1和2.19,在参考类似文献的基础上,初步考虑用Poisson回归来拟合数据。不过,本案数据有比较特殊的地方,对变量ABSENT做简单变换,变换后的ABSENT服从对称分布。因此,在本案数据的回归拟合中,在考虑Poisson回归方程的同时,也考虑普通线性回归方程,取这两个模型中对数似然比显著的那个。
模型的实际意义在于,可能会更频繁出现缺勤现象的雇员主要是那些工作复杂程度低、对主管有意见、在嘉泰公司工作时间较短的人。公司可以通过适当增加工作来降低缺勤率。
二、建模过程
严格地说,在影响缺勤率的7个因素中,除PAY外,其余6个变量均非连续变量。不过,在具体的统计应用实践中,当非连续变量的取值超过15个时,可以把该变量当作连续变量处理,这种处理变量的近似方法Jorgensen在其书中也有提及。这样,上述7个影响因素中,JOBCLAS、COMPLX、PAY、SENIOR、AGE可被看作是连续变量,SATIS和DEPEND是分类变量。
Spearman 秩相关分析的结果表明(显著性水平为0.1):
●ABSENT与变量JOBCLAS正相关,即员工的JOBCLAS越高,其缺勤的可能性越大。不过,该相关关系并不显著。
●ABSENT与变量COMPLX间显著负相关,即员工工作的复杂程度越低,其缺勤率可能越高。
●ABSENT与变量PAY间显著负相关,即员工的基本薪资越低,其缺勤率可能越高。
●ABSENT与变量SATIS间显著负相关,即员工对其主管的满意度越低,其缺勤率可能越高。
●ABSENT与变量SENIOR间显著负相关,即员工在嘉泰公司的工龄越短,其缺勤率可能越高。
●ABSENT与变量AGE间显著负相关,即员工的年龄越小,其缺勤率可能越高。
●ABSENT与变量DEPEND负相关,即员工需要赡养的人越少,其缺勤率可能越高。不过,该负相关关系不显著。(见下表)。
从上面的分析中可以看出,变量ABSENT与其余7个变量中的5个存在显著的相关关系,因此可将这5个变量初步选为回归方程的自变量。
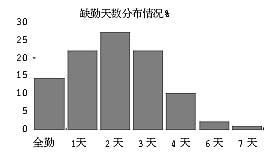
由于ABSENT是一个计数因变量,不满足普通线性回归方程拟合中正态因变量的假定,因此从严格的意义上说,本案数据不能建立普通线性回归方程。同时,由于变量ABSENT的均值和方差分别约为2.1和2.19,在参考类似文献的基础上,初步考虑用Poisson回归来拟合数据。
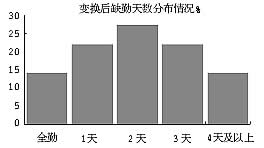
不过,本案数据有比较特殊的地方,对变量ABSENT做简单变换,变换后的ABSENT服从对称分布(下图)。因此,在本案数据的回归拟合中,在考虑Poisson回归方程的同时,也考虑普通线性回归方程,取这两个模型中对数似然比显著的那个。
由于变量PAY的系数为正,这与前面提到的变量ABSENT与变量PAY间显著负线性相关矛盾,怀疑自变量间可能存在共线性,这一点由变量complx,pay,senior,age 4个自变量的Pearson线性相关系数得到证实(下表)。
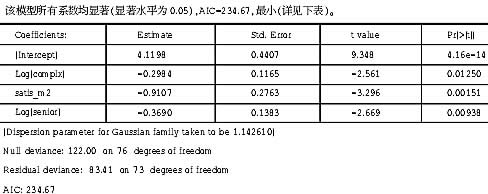
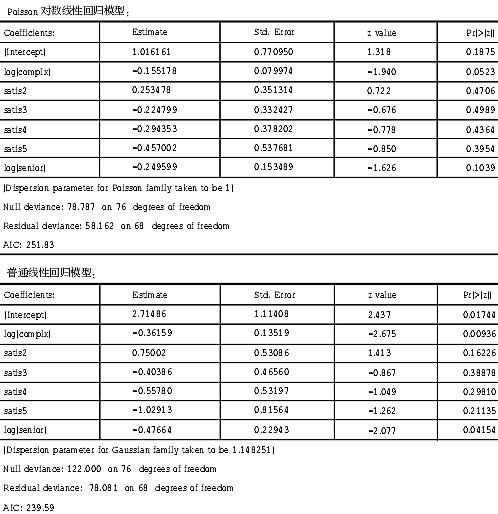
不过,线性相关关系显著并不构成舍弃这4个自变量中的一个或者几个的理由,在下面的分析中,对变量COMPLX和SENIOR做对数变换,拟合Poisson对数线性回归模型以及普通线性回归模型。结果如下:
两者对比,显然普通线性回归模型的对数似然比显著,即普通线性回归方程更适合本案数据。
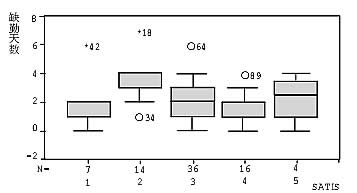
另外,从上表中可以看出变量SATIS取2时,缺勤率会增加,而SATIS取3、4、5时,缺勤率却会降低。再参考下图,考虑引入二元哑变量SATIS_M,当SATIS_M=0时表示“对主管有意见”,而当SATIS_M=1时表示“对主管无意见”,拟合普通线性回归方程。
当自变量为Ln(COMPLX)、ln(SENIOR)、AGE、PAY、SATIS_M时,拟合普通线性回归模型,以AIC为模型选择的标准,在下列四个模型中进行取舍:
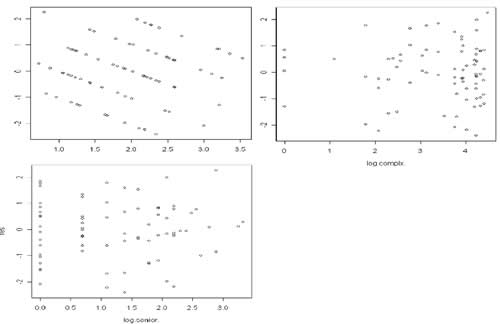
从下面三个残差诊断图中可以看出,上面所拟合的模型仍未能被认为是最好,这个问题可能来自于最初所设计的影响因素不太全面,例如并未统筹考虑人口特征、工作压力、生活压力、个性特征、工作部门等方面因素来挑选可能的影响因素。