摘要

　　本文立足我国二线城市，从河南的省会城市郑州的市调公司满意度模型参数估计方法应用情况入手，结合实例，分析了二线城市常用的传统回归方法的应用与主成分回归方法的优势互补方案，同时，又深入浅出地介绍了目前技术已经比较成熟的结构方程模型和偏最小二乘法的基本原理及其应用。

　　笔者认为，在实际满意度研究过程中，将多种参数估计方法结合起来使用，能收到更好的效果。

　　关键词：满意度模型参数估计回归主成分结构方程模型偏最小二乘


　　引文

　　满意度研究是当前市场调研的热点，很多企业需要定期进行满意度调研，并将其结果作为全面质量管理和客户关系管理的重要信息来源，以获取市场竞争优势。

　　河南君友商务咨询公司是较早涉足满意度研究领域的专业研究型公司，已为多个客户做过满意度项目，既有长期定量监测，也有神秘顾客等方式。实践表明，满意度研究最重要的工作是建立科学的满意度模型，而满意度模型的参数估计则更是重中之重。

　　因此，本文试图在现有满意度模型参数估计方法的基础上，结合实际应用情况，对比分析各种参数估计方法的特点，以便在今后满意度测评中，针对不同满意度模型选择合适的参数估计方法。

　　一、二线城市满意度模型参数估计方法的应用


　　目前，我国二线城市大多数市调公司主要还是采用回归分析来进行满意度模型的参数估计。

　　回归分析（Regresion）是通过分析数据拟合因变量与自变量之间的关系式，来检验影响变量的显著程度。例如，利用多元线性回归，建立满意度模型方程“总体满意度=a+b1*产品满意度+b2*服务满意度+b3*价格满意度”。一般情况下，通过上述方程就可以分析各环节满意度对总体满意度的影响，相类似的，我们也可以分析一些细项对各环节满意度的影响。

　　因此，回归分析可以算得上是一种有效且易用的方法。但是，在使用回归分析方法时，一定要注意其技术本身所存在的一些局限性：


　　回归分析的局限性

　　首先，回归分析无法解决多重共线的问题。

　　多重共线指的是多个变量之间存在相关甚至高度相关，这种现象在实际调研中是经常出现的，但回归分析无法解决这一问题。例如，在一项关于乘客对乘车环境的满意度研究中，得到这样一个回归方程，Y=0.276+0.073*站内环境+0.053*乘车方便性-0.042*站内安全感+0.033*车内环境-0.023*乘车方便性+0.022*广播质量+……。这个方程有个很奇怪的地方，站内安全感和乘车方便性对总体满意度的影响是负向的，这是有悖于常理的结果，也可以说是不正确的结果。出现这样结果的主要原因是自变量之间存在高度相关，也就是所谓的多重共线性的问题。

　　我们可以用图来说明多重共线性问题：

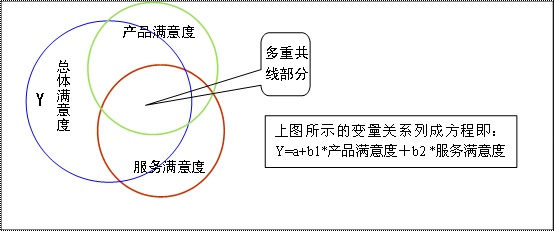
　　从上图可以看到，产品满意度和服务满意度之间有很大一部分重叠，这就是多重共线部分。由于多重共线的问题，此时的b1、b2两个标准回归系数已不能被用来准确地说明两个自变量对因变量作用的大小。同时，由于多重共线的问题，回归方程估计的系数会非常不稳定，不同样本得到的回归系数会有很大差异，从一个样本得到的回归系数推广到总体时，结果就很不可靠。所以说，多重共线的问题是多元回归技术无法解决的严重问题之一。

　　其次，回归方法使用的前提假设条件是各观测变量不存在测量误差，即各观测变量都已被百分之百真实测量出来，而这一假设在测量理论和实际操作中都是不可能满足的。经典测量理论认为：测验分数＝真分数＋误差分数，误差分数是无法避免的。同样，在实际操作过程中，系统误差和随机误差也是人力和主观愿望所无法控制的，但回归方法由于其方法本身的局限无法解决这一问题。所以，如果测量误差越大，回归分析所得结果的误差也越大。

　　除了多重共线和测量误差的问题之外，回归方法还存在无法同时考察多个因变量的问题等。那么，针对这些问题，市调公司是如何解决的呢？


　　优势互补：主成分回归

　　为了解决回归分析方法的多重共线问题，部分市调公司适时地引入了主成分回归分析方法（Principal component regression，PCR）。主成分回归分析的实质是将主成分分析与回归分析结合起来使用。具体使用步骤如下：

　　首先利用主成分分析产生若干个主成分。在这个过程中，那些相关性较强的变量就会被综合在一个主成分中，而不同的主成分之间又是相互独立的。

　　然后，以这些主成分为自变量进行多元回归分析，此时就不会再出现共线的问题。

　　举例具体说明如下：

　　对产品满意度而言，可能有产品性能、性能稳定性、硬件质量、配置合理性、外观造型、颜色搭配、产品说明等测量指标，但是相关分析发现，部分变量之间存在较高的相关，那么，直接进行回归分析就会由于多重共线的问题而造成结果不稳定，此时，就可以通过主成分回归方法来解决：

　　第一步：先进行主成分分析，得到两个主成分，如下图：

　　第二步，再以这两个主成分为自变量、产品满意度为因变量建立回归模型：

　　这样，主成分回归就解决了多重共线的问题，从这点来看，主成分回归比传统回归分析又前进了一步。但主成分回归没有解决测量误差的问题。

　　如何解决测量误差问题？目前，二线城市的客户要求还达不到这样的高度，但在一线城市，大型市调公司面对高端客户时就必须考虑这样的问题。在此，笔者介绍两种主流的满意度模型参数估计方法，以供大家参考。

　　二、主流的满意度模型参数估计方法


　　在满意度模型的参数估计方法中，技术比较成熟且有一定影响力的有结构方程模型和偏最小二乘法等。


　　结构方程模型(Structural Equation Model，SEM)

　　结构方程模型是在己有的因果理论基础上，用与之相应的线性方程系统表示该因果理论的一种统计分析技术，其目的在于探索事物间的因果关系，并将这种关系用因果模型、路径图等形式加以表述。一般而言，结构方程模型分为测量模型与结构模型：

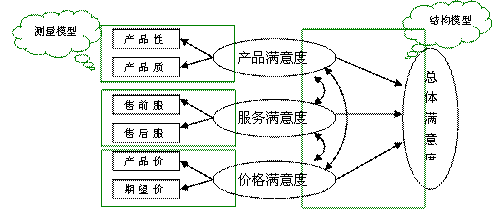
　　如上图所示，测量模型分析的是测量变量与潜变量之间的关系；而结构模型分析的是潜变量与潜变量之间的关系。结构方程模型以协方差矩阵匹配的策略为基本思路，对模型参数进行整体估计，从而可以解决变量间多重共线的问题。同时，结构方程模型可以在模型设定时将各观测变量的误差项一一注明，从而给出更符合理论要求和实际操作情况的结论。

　　结构方程模型可以借助一些软件来实现，目前流行的有Amos、Lisrel等。例如，利用Amos4.0设计关于员工工作表现模型，根据理论，我们假设，影响员工工作表现的因素包括相关知识，工作价值，以及对工作的满意度。进行实地访问，得到数据，根据数据间的协方差矩阵与假设模型的协方差矩阵的匹配程度，估计参数如下图：

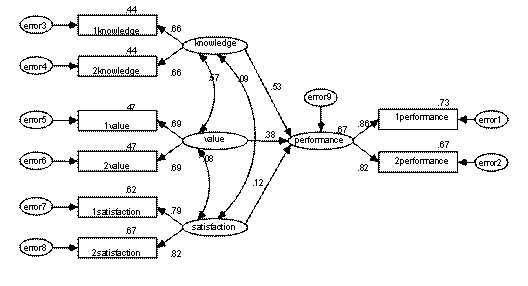
　　与传统回归相比，结构方程模型有很大的优势：首先，它可以有效地解决变量间多重共线和测量误差的问题；其次，它可以充分考虑多因变量的问题；其三，它能够很好地体现调研人员的专业和理论思维能力。最后，结构方程模型最大的优点就是可以整体、综合地分析变量间的关系，从而得到更为可靠的结果。

　　但应用结构方程模型，也需要满足一定的要求：

　　结构方程模型一般要求比较大的样本容量。确定样本容量大小，需要考虑的问题之一是潜变量与观测变量的数目，变量的数目越大，所需的样本容量也就越大。

　　观测变量的分布服从多元正态分布。如果所有的观测变量都服从多元正态分布，则只需较小的样本容量。Bentler和Chou（1987）建议，如果所有变量都服从正态分布，样本容量与自由参数数目的比值达到5:1就够了；如果变量非正态分布，需要较大的样本容量才有可能获得准确结果。

　　但对于顾客满意度和各个结构变量之间存在的非线性关系，以及模型中测评变量存在较严重的偏态情况（如，各观测变量明显的偏离于正态分布），结构方程由于自身的局限性不能很好的处理，这时就需要引入偏最小二乘法。


　　偏最小二乘法(Partial Least-Squares Method，PLS)

　　偏最小二乘法是集多因变量对多自变量的回归建模以及主成分分析为一体的多元数据分析方法。这种算法最初由H.Wold在1966年提出并应用于经济学中。

　　偏最小二乘法的整体模型如下图：

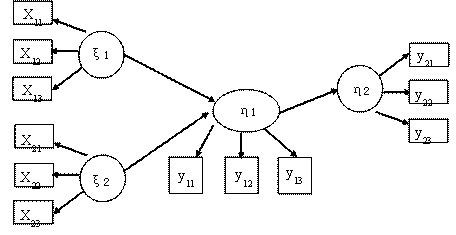
　　从偏最小二乘法整体模型来看，与结构方程模型非常类似，但二者在具体估计方法上有差异：

　　首先，结构方程模型利用极大似然法估计和最小二乘法估计模型参数，偏最小二乘法使用偏最小二乘的方法估计模型参数；其次，偏最小二乘法采用的估计策略是首先估计每一个潜变量与其对应的观测变量的关系，然后考察各个潜变量之间的关系；结构方程模型是通过匹配假设模型的协方差矩阵与数据的协方差矩阵，同时整体估计所有参数。这样，从分析的整体性上来看，偏最小二乘法逊色于结构方程模型。但是由于偏最小二乘法可以处理非线性关系与非正态分布指标，其适用性要优于结构方程模型。

　　从基本估计方法上看，偏最小二乘法与前面的主成分回归很相似，二者都抽取了主成分，只是提取主成分的方法不同。简而言之，主成分回归使用的是自变量之间的协方差，偏最小二乘法使用的是自变量与因变量之间的协方差。

　　密西根大学的MichaelD.Johnson和Anders Gustafsson用实例对两种方法进行比较。结果发现，两种方法得到的结果是非常相似的。如下图所示：

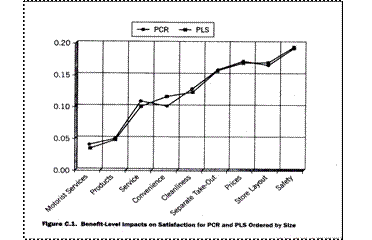
　　比较两种方法估计结果的残差发现，偏最小二乘法计算所得的拟合残差较小,稳定性高。可见，偏最小二乘法的优势是很明显的。但由于偏最小二乘法实现起来较为困难，所以只有少数的市调公司在使用。

　　小结


　　综上所述，传统回归与主成分回归分析方法简单易行，但其局限性较大，在使用时尤其要注意其共线性与误差处理问题；结构方程模型与偏最小二乘法在满意度模型参数估计中各有优势，两者在精度估计上均优于回归分析方法，但也同时存在一些问题。综合几种方法在满意度模型参数估计时的特点（见下表）：

	传统回归	主成分回归	结构方程模型	偏最小二乘法
多重现性的问题	不能解决	可以解决	可以解决	可以解决
是否考虑测量误差	没有考虑	没有考虑	考虑了	考虑了
对数据及分布要求	线性	线性	线性，正态分布	没有要求
是否可以计算潜变量	不可以	可以	不可以	可以
实现难度	没有难度	没有难度	没有难度	有一定难度

　　在实际满意度测评时，应根据数据特点及应用要求来选用合适的参数估计方法。如果一种参数估计方法不能达到目的，将多种方法结合起来使用是一种不错的解决方案。

　　例如在美国，顾客满意度模型的建模就是将偏最小二乘法和结构方程模型结合起来使用：首先通过偏最小二乘法抽取主要的潜变量，并估计出潜变量的值，以利于综合的比较；然后，利用结构方程模型构建整体模型，重点考察变量间的关系。

　　在国内，北京一家大型市调公司在进行一项多产品的客户满意度研究时，也是同时使用了结构方程模型与偏最小二乘法两种方法。它首先利用结构方程模型进行整体分析，然后利用偏最小二乘法计算出不同类别产品的满意度指数，这样既可以实现满意度监测的横向比较，又可以实现对不同时期的满意度指数进行纵向比较，最终为该产品企业制订整体发展战略提供了非常有价值的参考资料。

　　实际上，还有很多有价值的参数估计组合方法有待开发。作为市调公司，我们将本着为客户负责的原则，在仔细分析满意度模型及数据特点的基础上，选用合适的参数估计方法或方法组合，提高调研结果的精度，以求为客户提供更多有价值的信息。

　　主要参考资料：


　　·肖琳，何大卫.PLS回归方法及其医学应用,中国卫生统计[J],2004,4,19(2):76-79

　　·侯杰泰.为何需要结构方程模式及如何建立潜伏变项,教育研究学报[J],1994，9（1）：87-92

　　·温忠麟，侯杰泰等.结构方程模型检验:拟合指数与卡方准则,心理学报,2004,36(20:186-194

　　·韩金山,等.系统的pls方法在满意度实证研究中的应用,运筹与管理,2005,10

　　·梁燕.顾客满意度指数模型及其参数估计方法,统计研究

　　·金勇进，梁燕.偏最小二乘(PartialLeastSquare)方法的拟合指标及其在满意度研究中的应用.数理统计与管理[J].2005，24(2):40-44

　　·孙连荣.结构方程模型SEM的原理及操作,宁波大学学报（教育科学版）

　　·肖琳，何大卫.PLS回归方法及其医学应用.中国卫生统计